2010-10-29

カオス現象(その 2)

前回導き出した漸化式
$y_{n+1}=ay_n(1-y_n)$
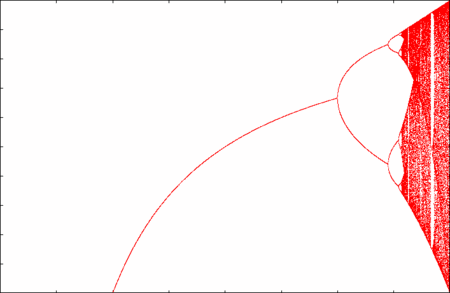
がどんな挙動をするのか、論より証拠、次の画像を見てください。

これは、初期値を $y_0=0.1$ として、横軸に $a$ を取り 0.001 刻みで動かし、十分大きい $n$ から先の $y_n$ の値を 100 個プロットしたものです。

最初のうちはある値に収束していくことが見てとれます。 $a$ が 3 のあたりで二手に分かれ、2 周期点が現れます。その後 4 周期点、8 周期点…と分岐していき、最後にはもはや周期など見てとれない、全く予測不可能な挙動をしていることが分かります。

機械計算による丸め誤差のせいではないか、と思う人もいるかもしれませんが、実はそうではないのです。次回はその秘密に迫ってみます。

2010-10-27

カオス現象(その 1)

数学・解析

$\frac{dx}{dt}=(b-cx)x$ … (*)
という微分方程式を考えてみます。これは 1 階の微分方程式で変数分離形なので解析的に解くことができます。実際、初期値を $x(0)=x_0$ とすると
$x(t)=\frac{bx_0 e^{bt}}{b+cx_0(e^{bt}-1)}$
となります。ところで、(*) を Euler 法で近似的に解くことを考えてみましょう。微小の刻み幅 $h$ を固定して考えると
$\frac{x(t+h)-x(t)}{h}=(b-cx(t))x(t)$
で、 $1+bh=a,\frac{ch}{1+bh}x(t)=y(t)$ とおいて整理すると
$y(t+h)=ay(t)(1-y(t))$
となります。そこで $y_0=y(0)=\frac{ch}{1+bh}x_0$ から始めて $y_n=y(nh)$ とおくと
$y_{n+1}=ay_n(1-y_n)$
という漸化式を得ます。この漸化式が実に興味深い挙動を見せてくれるのですが、続きはまたの講釈で。

2010-10-21

有限値に収束するが、微分が収束しない関数

数学・解析

$C^1$ 級の関数 $f(x)$ があって $f(x)\to M(x\to\infty)$ のとき、直感的には $f'(x)\to 0(x\to\infty)$ になりそうな気がします。しかし
$f(x)=\frac{\sin x^2}{x}$
とおくと生憎そうはなりません。 $f(x)\to 0(x\to\infty)$ ですが
$f'(x)=2\cos x^2-\frac{\sin x^2}{x^2}$
で、 $2\cos x^2$ の項が収束しない(強制振動)ので、 $f'(x)\to 0(x\to\infty)$ とならないのです。

直感に頼ると痛い目にあうという好例でした。

2010-10-19

共分散の落とし穴

数学・確率・組み合わせ

二つの確率変数 X , Y が独立なら、共分散
$Cov(X,Y)=E(XY)-E(X)E(Y)$
は 0 になりますが、共分散が 0 だからといって独立になるかというとそうではありません。

例えば X を標準正規分布に従う確率変数とし、 $Y=X^2$ とおきます。このとき $E(X)=E(X^3)=0$ なので
$Cov(X,Y)=E(X^3)-E(X)E(X^2)=0$
ですが、明らかに X と Y は独立ではありません。

2010-10-16

三角関数の問題

数学・解析

$x$ は方程式 $3\sin x+4\cos x=5$ の解で $0\lt x\lt \frac{\pi}{2}$ とする. このとき $2\sin x+\cos x+4\tan x$ の値を求めよ.

という問題を某所で教えてもらったのでちょっと解いてみました。

まず方程式を
$\frac35\sin x+\frac45\cos x=1$
と変形し、 $\sin\alpha=\frac45,\cos\alpha=\frac35$ を満たす $\alpha(0\lt\alpha\lt\frac{\pi}{2})$ を用いて
$\sin(x+\alpha)=1$
とします。 $0\lt x+\alpha\lt \pi$ なので、これを満たすのは
$x+\alpha=\frac{\pi}{2}$
のみです。したがって $x=\frac{\pi}{2}-\alpha$ となります。これを $2\sin x+\cos x+4\tan x$ に代入すると
$\begin{align}2\sin x+\cos x+4\tan x&=2\sin(\frac{\pi}{2}-\alpha)+\cos(\frac{\pi}{2}-\alpha)+4\tan(\frac{\pi}{2}-\alpha)\\&=2\cos\alpha+\sin\alpha+\frac{4}{\tan\alpha}\\&=2\cdot\frac35+\frac45+\frac{4}{4/3}\\&=\frac65+\frac45+3=5\end{align}$
と綺麗な値になりました。

高校レベルの数学しか使わないので、ぜひ高校生に挑戦してほしい問題だと思いました。まぁここに答書いちゃいましたけどね(笑)。

2010-10-15

f(x + y) = f(x) + f(y) を満たす関数

数学・解析

タイトルのような関数で連続なものは $f(x)=cx$ ( $c$ は定数)しかありませんが、連続の代わりに
$x\gt 0\Rightarrow f(x)\gt 0$ … (*)
という条件を付けても同じ結果が得られます。

まず、 $f(x+y)=f(x)+f(y)$ ならば、 $f(1)=c$ とおいて、任意の有理数 $r$ に対して $f(r)=cr$ となることが分かります。

さて、(*) の条件を付け加えます。任意の実数 $x$ に対し $r_0\lt x\lt r_1$ を満たす有理数 $r_0,r_1$ が存在します。そして (*) の条件と
$f(x)=f((x-y)+y)=f(x-y)+f(y)$
から $f(x-y)=f(x)-f(y)$ に注意して
$\begin{array}{lcl}x\gt y&\Rightarrow&x-y\gt 0\\&\Rightarrow&f(x-y)\gt 0\\&\Rightarrow&f(x)-f(y)\gt 0\\&\Rightarrow&f(x)\gt f(y)\end{array}$
と $f(x)$ の単調性が導けますから
$r_0\lt x\lt r_1\Rightarrow cr_0=f(r_0)\lt f(x)\lt f(r_1)=cr_1$
が成り立ちます。一方で $c=f(1)\gt 0$ なので
$r_0\lt x\lt r_1\Rightarrow cr_0\lt cx\lt cr_1$
も成り立ちます。故に
$-c(r_1-r_0)\lt f(x)-cx\lt c(r_1-r_0),$
すなわち
$|f(x)-cx|\lt c(r_1-r_0)$ … (**)
が成り立ちます。

ところで、 $r_0\lt x\lt r_1$ を満たす有理数 $r_0,r_1$ について、 $r_1-r_0$ はいくらでも小さくできるので、(**) の右辺はいくらでも小さくできますから $f(x)=cx$ が成り立つことが分かります。

ちなみに (*) の代わりに
$x\gt 0\Rightarrow f(x)\lt 0$
という条件を付け加えても同じ結果が得られます。

2010-10-13

三角加法関数展開形

数学・代数

$\sin(x_1+\dots+x_n)$ を加法定理を用いて展開すると、 $S_1=\sin x_1,\dots,S_n=\sin x_n,C_1=\cos x_1,\dots,C_n=\cos x_n$ の $2n$ 変数の多項式になりますが、その一般形を探ってみたら面白いのではないか、という話を、先日知り合いの方と話していました。例えば
$\sin(x_1+x_2)=S_1 C_2+S_2 C_1,$
$\sin(x_1+x_2+x_3)=S_1 C_2 C_3+C_1 S_2 C_3+C_1 C_2 S_3-S_1 S_2 S_3$
$\sin(x_1+x_2+x_3+x_4)=\\S_1 C_2 C_3 C_4+C_1 S_2 C_3 C_4+C_1 C_2 S_3 C_4+C_1 C_2 C_3 S_4\\-S_1 S_2 S_3 C_4-S_1 S_2 C_3 S_4-S_1 C_2 S_3 S_4-C_1 S_2 S_3 S_4$
となります。一般に
$\sin(x_1+\dots+x_n)=f_n,\cos(x_1+\dots+x_n)=g_n$
とすれば
$f_{n+1}=f_n C_{n+1}+g_n S_{n+1},g_{n+1}=g_n C_{n+1}-f_n S_{n+1}$
となるので、この漸化式をもとに一般形は求められそうな気はしますが、はて…。